E: Perhaps the most unappreciated number

[Deathraider]

Today is 2/7, a holiday known as e day. e=2.71828182845904523536028747135266249775724709369995...

But what is e?

Origins:

There's a formula to calculate the exponential growth of interest. Given P is the original input, A is the output, with t being time, r being your interest rate, and n being how often you're being paid, this is the formula:

Bernoulli wondered about this question:

Imagine you start with a dollar, and in 1 year, I give you a dollar. You now have 2 dollars.

Suppose instead I gave 50% every 6 months. Then you'd start with a dollar, you'd go to a $1.50, then $2.25. So you made more money. Suppose I paid you 1/12 every month, how much would you have? About $2.61 dollars. Suppose I did this more and more often. Suppose at every instant I paid you an infinitesimal amount. What does this value approach. That's e.

You might be saying how this number is even useful. Sure, it helped with a theoretical problem, but there's no such bank that would ever do that. Well here's the cool thing: While the equation for interest rate is about discrete payments, e is actually describing continuous growth. Suppose I wanted to model bacteria growth. How would I do that? Well the amount of bacteria after some given time is equal to Ae^kt, where A is your starting amount, k is some constant, t is time, and e is Euler's number.

Wait, why is it called Euler's number is Bernoulli discovered it?

Enter Euler

Now Euler is a pretty cool dude in mathematics. We knew of numbers called imaginary numbers, the square roots of negative numbers. They complete Algerbra. We also know of Taylor series. Taylor series are actually really cool because they're these infinite sum that are like polynomial that with finite terms can approximate a curve. If you added more and more terms, you'd get closer and closer to the true value.

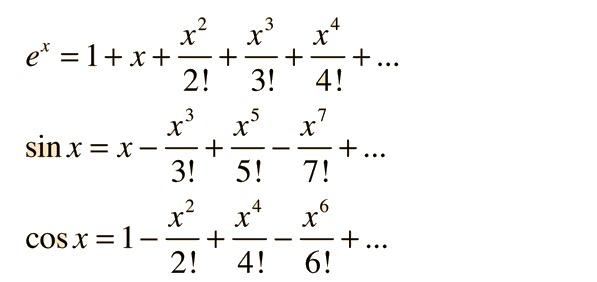
Euler is really genius when he used Taylor series and imaginary numbers to come up with a formula. Here's the basics of the imaginary number (i). i^1=i,i^2=-1, i^3=-i, i^4=1 and it repeats. Substituting ix in the Taylor series of e, he gets out cos(x)+isin(x).

So happy e day everybody!

[IlyaTheImpaler]

I don't think it is unappreciated, it appears very frequently in pop culture, I see it every time I watch some random tvshow that has some math in it lol

Since you are at the Taylor series of exp (x), when I was your age there was a popular exercise to show that e cannot be a solution to a0 + a1 x + a2 x^2 +... + an x^n = 0 (where n is any natural number, a0, a1..., an are integers and a0 is nonzero). It was so that us kids understand e is something quite... different (for some context, if your civilization starts from the simplest counting numbers, the idea of negative numbers is conceivable to you, since you can get -1 by defining the root of x + 1 = 0 as a new number, rational numbers are also conceivable to you, you can get something like 1/2 by defining the root of 2x - 1 = 0 as a new number, irrational numbers are also conceivable, if you want sqrt (2) you define a root of x^2 - 2 = 0 as a new number, imaginary numbers are also conceivable and you can get to complex numbers by defining a root of x^2 + 1 = 0 as a new number, pi is stranger, but still conceivable, you can draw a circle and define the ratio of circumference to diameter as pi,... BUT your civilization would never be able to even imagine something like e exists if all they could do is algebra and geometry 😂). The math involved in this exercise was also quite different (from the usual Calculus exercise, even though it's technically just Calculus of function of one variable)

[Deathraider]

e and pi are transcendental! All hail e and pi!

[PrincessGrail]

That could be very useful in figuring out how interest accrues in your trust fund.

Have you ever heard of a mathematician named Armand Borel?

[Deathraider]

No, I have not.

[PrincessGrail]

Ok. Cool.

[Deathraider]

Who is he?

[PrincessGrail]

He is a famous mathematician. And my ex’s grandfather.

Thanks for MHO.

[Deathraider]

Wait what? Did you see his works?

[PrincessGrail]

I met him once. He invented something called the Borel set.

[Deathraider]

Cool! Lucky you.

[sarahhcmarie]

damn dude you just fucked my brain up

[Deathraider]

Why aren't you so e-xcited?

[sarahhcmarie]

boooo
bad joke

[WhiteSteve]

If I could instill any knowledge into anyone’s brain, especially at a young age, it’s the concept of compounding interest. Invest—>reinvest—>repeat—>retire comfortably, and maybe even early👏👏👏

[jacquesvol]

Its because of the compound interest that the FED and the ECB keep interest rates near zero.

That's addictive for indebted ccompanies and countries.

You won't see interest rates going up again that soon.
Too bad for your pension fund :p

[jacquesvol]

Interests due on personal debt will not go down.
That permits banks to get a more solid fiinancial structure and to avoid a 2nd 2008 crisis.

[Aguysopinion4799]

This gave me such a headache to wrap my head even a tad around it... (BRAIN) *CURRENTLY... IN REPAIR*

[WhereAmI]

Imaginary numbers are a great way to alienate people. Nobody cares, dood.

I should know, I’m an EE. 😂

[Deathraider]

Hmmm, yeah. Imamaginary numbers aren't useful.

Except electrical engineering, fluid dynamics, cartography, vibration analysis, electromagnetism, relativity and quantum mechanics.

[WhereAmI]

I didn’t say they weren’t useful. Most people who don’t live in those worlds find them boring af. 😂

[DollySummers]

Huh I guess you’re right that umber is good. I still prefer eight.

[John_Doesnt]

E is known as the virgin variable, the more familiar you are with E the more likely you are a virgin.

[PrettyRegular]

Cool. I love math, but right now I'm not in the mood. I can calculate very well on my head, so I can go pretty far without formulas.. At least in basics. 😃

[sp33d]

For your age, you know an impressive amount of analysis terminology. Well done.

[Deathraider]

I wished I wrote more about e. Like how it's derivative and intergral are the same, or how it relates to approximating the factorials. Or how it pops up in probability.

I'll just wait for e day next year.

[sonnysunshine]

Even Einstein marveled at the magic of compound interest.

[ChiPaPa]

I see mathematician in your future.

[Secretgardenblood]

Good take

[Anonymous]

Great

[Anonymous]

Cool

[Anonymous]

Interesting