An irrational constant (like Euler's number e, and pi - 3.14159265...) that occurs frequently in nature, the Golden Ratio (also known the golden mean, golden section) is best summarised by stating that the lengths a and b are to a, as a is to b (see diagramme below).
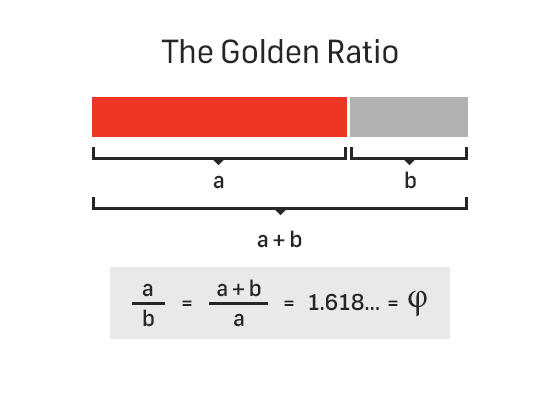
Symbolised by the Greek lower case letter 'phi', the ratio is also observed in the Fibonacci sequence, a sequence that is produced when one takes two terms that are then added together to produce the next term within, beginning at one (i.e. 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144...). The significance of this ratio is that it can be, and is, found in the most unexpected of places (ex. a flower will often have a Fibonacci number of petals), and perhaps underlies the very nature of reality itself. In the clip below, it's mentioned that the relationship between the Earth and the moon is defined by it (at the approx. 15:06 mark), and as we all know, during an eclipse of the sun by the moon, the moon from our perspective on Earth appears to be the exact same size as the sun, covering it perfectly and leaving only the corona visible.
This video isn't as long, and explains it very well.
Most Helpful Opinions